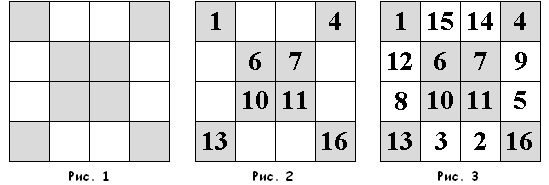
Магические квадраты — это увлекательная игра-головоломка, которая требует логики и математических навыков. В этой статье мы расскажем о том, как играть в магические квадраты и предоставим несколько примеров и способов решения.
В следующих разделах статьи мы рассмотрим основные правила игры, различные виды магических квадратов, а также поделимся советами и стратегиями для успешного решения головоломок. Кроме того, мы расскажем о истории магических квадратов и их применении в различных областях, таких как математика, криптография и искусство. Присоединяйтесь к нам и окунитесь в увлекательный мир магических квадратов!
Основы магических квадратов
Магические квадраты – это особые квадратные таблицы, в которых числа располагаются таким образом, что сумма чисел в каждой строке, столбце и диагонали одинакова. Эти удивительные структуры имеют древние корни и были изучены и использованы в различных культурах по всему миру.
Основные характеристики магического квадрата:
- Квадратная форма: все стороны таблицы имеют одинаковую длину.
- Размерность: магические квадраты могут быть разных размеров, например, 3×3, 4×4, 5×5 и т.д., где число указывает количество строк и столбцов.
- Уникальность чисел: каждое число в квадрате должно быть уникальным и не повторяться.
- Магическая сумма: сумма чисел в каждой строке, столбце и диагонали должна быть одинаковой и называется магической суммой.
Магические квадраты могут быть решены различными способами. Существуют алгоритмы и методы, позволяющие создавать магические квадраты разных размеров. Однако, для создания магического квадрата требуется определенное математическое и логическое мышление. Часто магические квадраты решаются с использованием компьютерных программ, которые автоматически генерируют квадраты определенного размера.
Изучение магических квадратов может быть интересным и увлекательным занятием. Они имеют множество математических и эстетических свойств, которые могут быть исследованы и изучены. Кроме того, магические квадраты могут быть использованы в различных играх и головоломках, что делает их еще более интересными и привлекательными.
Как решать магический квадрат
Что такое магический квадрат?
Магический квадрат — это квадратная таблица, заполненная целыми числами, таким образом, что сумма чисел в каждом столбце, строке и диагонали одинакова. Это является основным свойством магического квадрата.
Магические квадраты имеют долгую историю и были известны уже в древности. Их использовали в различных культурах, включая древний Китай, Индию и Египет. В современном мире магические квадраты широко используются в математике, головоломках и даже в магии.
Основные характеристики магического квадрата:
- Квадратная форма: магический квадрат всегда имеет одинаковое количество строк и столбцов.
- Целые числа: каждая ячейка магического квадрата содержит целое число.
- Уникальные числа: все числа в магическом квадрате должны быть различными.
- Сумма строк, столбцов и диагоналей: сумма чисел в каждой строке, столбце и диагонали магического квадрата должна быть одинакова.
Пример магического квадрата:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
В этом примере сумма чисел в каждой строке, столбце и диагонали равна 15. Это делает его магическим квадратом порядка 3.
Магические квадраты могут иметь различные порядки, то есть различное количество строк и столбцов. Например, порядок 3 означает, что квадрат имеет 3 строки и 3 столбца. Чем выше порядок, тем сложнее построить магический квадрат.
История магических квадратов
Магические квадраты – это особые квадратные таблицы, заполненные числами таким образом, чтобы сумма чисел в каждой строке, столбце и диагонали была одинаковой. Эти фантастические конструкции заинтересовали людей на протяжении многих веков и имеют богатую историю.
Первые упоминания о магических квадратах можно найти уже в древних китайских и индийских источниках. Однако, ранние магические квадраты имели несколько отличные от современных. Например, в древних китайских квадратах использовались символы вместо чисел. Также, в некоторых культурах использовались квадраты не только размером 3х3, но и других размеров.
Первое описание магического квадрата в современном понимании было найдено в древнем индийском тексте "Катапаядаджна", датированном 7 веком нашей эры. Этот текст содержит описание магического квадрата 4х4 и демонстрирует его свойства. Открытие и описание этого квадрата считается важным моментом в истории магических квадратов.
С течением времени, магические квадраты стали известны в разных частях мира. Они привлекали внимание ученых, философов, математиков и даже мистиков. В Средние века магические квадраты были частью магических и астрологических практик, связанных с числами и символами.
В XVIII веке в Европе началась научная изучение магических квадратов. Ученые и математики начали искать различные свойства и закономерности в этих структурах. Они разработали различные методы и алгоритмы для создания и решения магических квадратов. Это привело к большему пониманию и использованию магических квадратов в математике и играх.
Сегодня магические квадраты продолжают быть объектом исследований и интереса. Они нашли применение в математике, криптографии, играх и даже искусстве. Знание и понимание истории магических квадратов помогает нам лучше понять и ценить эти удивительные структуры.

Правила игры в магические квадраты
Магический квадрат — это квадратная таблица, заполненная числами таким образом, что сумма чисел в каждой строке, столбце и диагонали одинакова. Это увлекательная головоломка, которая требует логического мышления и математических навыков. Давайте рассмотрим основные правила игры в магические квадраты.
1. Размер квадрата
Магический квадрат может иметь различные размеры, но наиболее распространены квадраты размером 3×3, 4×4 и 5×5. Размер квадрата определяет количество ячеек и чисел, которые нужно заполнить.
2. Числа
В магическом квадрате используются натуральные числа, начиная с 1 и постепенно увеличиваясь до n^2, где n — размер квадрата. Например, для квадрата 3×3 используются числа от 1 до 9, а для квадрата 4×4 — числа от 1 до 16.
3. Расстановка чисел
Числа располагаются в ячейках квадрата таким образом, чтобы сумма чисел в каждой строке, столбце и диагонали была одинаковой. Числа не могут повторяться в одной строке, столбце или диагонали.
4. Магическая сумма
Магическая сумма — это сумма чисел в каждой строке, столбце или диагонали магического квадрата. Для квадрата размером n, магическая сумма равна n * (n^2 + 1) / 2.
5. Заполнение квадрата
Процесс заполнения магического квадрата начинается с выбора любой ячейки в верхнем левом углу. Затем поочередно заполняются остальные ячейки, двигаясь вправо или вниз, и переходя на следующую строку или столбец, если достигнут конец текущей строки или столбца.
6. Методы заполнения
Существует несколько методов заполнения магического квадрата, включая методы "чет-нечет", "соединение" и "перестановка". Каждый из них требует определенной последовательности действий для достижения магической суммы.
7. Уникальность решения
Магический квадрат может иметь несколько различных решений, но все они будут иметь одинаковую магическую сумму и соответствовать правилам игры.
Игра в магические квадраты — это увлекательное занятие, которое помогает развивать логическое мышление и математические навыки. Попробуйте создать свой собственный магический квадрат и насладитесь этой умственной головоломкой!
Создание магического квадрата
Магический квадрат — это квадратная таблица, заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и по диагоналям одинакова. Создание магического квадрата может показаться сложной задачей, но с правильным подходом и некоторыми правилами это можно сделать.
Существует несколько методов создания магического квадрата, однако одним из самых простых и распространенных является метод "четных порядков". В этом методе квадрат имеет размерность, равную четному числу, например 4х4, 6х6 и т.д.
Шаг 1: Размещение чисел
Первый шаг в создании магического квадрата — размещение чисел в таблице. Начните с центральной ячейки верхней строки и поместите в нее число 1. Затем двигайтесь по диагонали вправо и вверх, размещая числа последовательно. Если вы достигаете края таблицы, переходите на противоположную сторону. Если ячейка уже занята, двигайтесь вниз вместо движения по диагонали.
Шаг 2: Заполнение оставшихся ячеек
После размещения всех чисел в таблице, заполните оставшиеся ячейки числами последовательно, двигаясь вниз и влево. Если вы достигаете края таблицы, переходите на противоположную сторону.
Шаг 3: Корректировка сумм
В конечном квадрате может возникнуть ситуация, когда суммы строк, столбцов и диагоналей не будут одинаковыми. Для исправления этого, вы можете заменить два числа в квадрате местами. Помните, что при замене чисел необходимо сохранить сумму каждого ряда и столбца.
Создание магического квадрата может потребовать некоторых расчетов и манипуляций, но с практикой вы сможете легко создавать квадраты разных размерностей. Эти квадраты могут использоваться в различных головоломках, играх и даже в некоторых магических трюках.

Выбор размера квадрата
Размер магического квадрата – это количество строк и столбцов в квадратной сетке. Он определяет, сколько чисел будет использовано в квадрате и какой будет общая сумма чисел в каждой строке, столбце и диагонали.
При выборе размера квадрата важно учитывать несколько факторов:
1. Число чисел
Количество чисел в магическом квадрате определяется размером квадрата по формуле: число чисел = размер^2. Например, для квадрата размером 3х3 будет использовано 9 чисел, а для квадрата размером 4х4 – 16 чисел.
2. Доступность чисел
При выборе размера квадрата также следует учесть доступность чисел. В классическом магическом квадрате используются числа от 1 до размера квадрата включительно. Например, для квадрата размером 3х3 используются числа от 1 до 9, а для квадрата размером 4х4 – числа от 1 до 16.
3. Сложность
Сложность магического квадрата может зависеть от его размера. Квадраты маленького размера, например 3х3 или 4х4, могут быть легче для расстановки чисел и нахождения решения. Квадраты большего размера, например 5х5 или 6х6, могут быть сложнее и требовать более тщательного анализа и расчетов.
Выбор размера квадрата зависит от ваших предпочтений и уровня опыта. Если вы новичок, рекомендуется начать с квадратов маленького размера, чтобы познакомиться с основами и получить опыт в решении простых задач. Постепенно можно переходить к квадратам большего размера и более сложным головоломкам.
Способы заполнения квадрата
Существует несколько способов заполнения магического квадрата. Каждый из них имеет свои особенности и требует определенных правил. Рассмотрим некоторые из них:
1. Метод Ло Шу
Метод Ло Шу является одним из самых старых способов заполнения магического квадрата. Он основан на китайской легенде о животном Ло Шу, которое является символом древней китайской магии. Для заполнения квадрата по методу Ло Шу необходимо следовать определенным шагам:
- Квадрат разделяется на равные ячейки.
- В центральную ячейку записывается число 1.
- Далее числа записываются по спирали, начиная с ячейки справа от центральной и двигаясь против часовой стрелки.
- Если ячейка уже занята, то число записывается в следующую свободную ячейку, двигаясь по спирали.
2. Метод Си Шу
Метод Си Шу основан на китайской философии и используется для создания магических квадратов большего размера. Для заполнения квадрата по методу Си Шу необходимо следовать следующим шагам:
- Квадрат разделяется на равные ячейки.
- В центральные ячейки записываются числа по порядку от 1 до N, где N — размер квадрата.
- Далее числа записываются по диагонали, начиная с ячейки справа от центральных и двигаясь вверх.
- Если ячейка уже занята или вышла за пределы квадрата, то число записывается в следующую свободную ячейку, двигаясь вниз.
3. Метод Франклина
Метод Франклина является более сложным способом заполнения магического квадрата. Он основан на математических принципах и требует выполнения определенных правил. Для заполнения квадрата по методу Франклина необходимо следовать следующим шагам:
- Квадрат разделяется на равные ячейки.
- В центральную ячейку записывается число 1.
- Далее числа записываются по определенным правилам, основанным на математической последовательности.
- Если ячейка уже занята, то число записывается в следующую свободную ячейку, двигаясь по определенному направлению.
Магические квадраты – тысячи лет восхищения // Vital Math
Проверка магического свойства
После того как мы заполнили квадрат числами, настало время проверить его на магическое свойство. Задача состоит в том, чтобы убедиться, что сумма чисел в каждой строке, столбце и диагонали равна одной и той же константе.
Для начала определим эту константу, которая является суммой всех чисел квадрата, деленной на размерность квадрата. Например, для 3×3 квадрата с числами от 1 до 9, сумма чисел равна 45, а размерность квадрата равна 3. Поделив 45 на 3, получим константу равную 15.
После определения константы, мы приступаем к проверке магического свойства. Для этого вычисляем сумму чисел в каждой строке, столбце и диагонали и сравниваем ее с полученной константой. Если сумма чисел в каждой строке, столбце и диагонали равна константе, то квадрат считается магическим.
Приведем пример проверки магического свойства для 3×3 квадрата:
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
В данном случае, константа будет равна 15. При вычислении суммы чисел в каждой строке, мы получим следующие значения:
- 2 + 7 + 6 = 15
- 9 + 5 + 1 = 15
- 4 + 3 + 8 = 15
Таким образом, сумма чисел в каждой строке равна константе 15. Проведя аналогичные вычисления для столбцов и диагоналей, мы также получим суммы, равные 15. Следовательно, данный квадрат является магическим.